Introduction to Celo epoch rewards and the target reward release schedule.
This page describes the historical Celo Layer 1 blockchain. It is useful for understanding Celo’s history, but does not reflect the current state of the network. As of block height 31,056,500 (March 26, 2025, 3:00 AM UTC), Celo has transitioned to an Ethereum Layer 2.
What are Epoch Rewards?
Epoch Rewards are similar to the familiar notion of block rewards in other blockchains, minting and distributing new units of CELO as blocks are produced, to create several kinds of incentives.
Epoch rewards are paid in the final block of the epoch and are used to:
A total of 400 million CELO will be released for epoch rewards over time. CELO is a utility and governance asset on Celo, and also the reserve collateral for Celo Dollar (and possibly in the future other whitelisted tokens). It has a fixed total supply and in the long term will exhibit deflationary characteristics similarly to Ethereum.
Reward Disbursement
The total amount of disbursements is determined at the end of every epoch via a two step process.
Step 1
In step one, economically desired on-target rewards are derived. These are explained in the following pages. Several factors can increase or decrease the value of the payments that would ideally be made in a given epoch (including the CELO to Dollar exchange rate, the collateralization of the reserve, and whether payments to validators or groups are held back due to poor uptime or prior slashing).
Step 2
In step two, these on-target rewards are adjusted to generate a drift towards a predefined target epoch rewards schedule. This process aims to solve the trade-off between paying reasonable rewards in terms of purchasing power and avoiding excessive over- or underspending with respect to a predefined epoch rewards schedule. More detail about the two steps is provided below.
Adjusting Rewards for Target Schedule
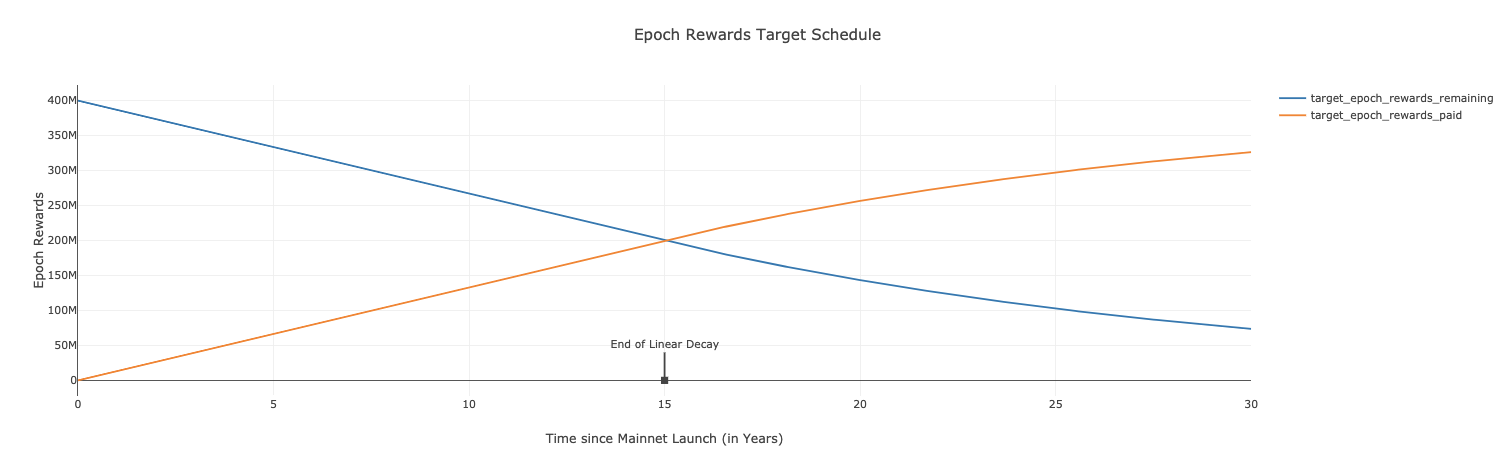
There is a target schedule for the release of CELO epoch rewards. The proposed target curve (subject to change) of remaining epoch rewards declines linearly over 15 years to 50% of the initial 400 million CELO, then decays exponentially with half life of h=ln(2)×15=10.3 afterwards. The choice of h guarantees a smooth transition from the linear to the exponential regime.
The total actual rewards paid out at the end of a given epoch result from multiplying the total on-target rewards with a Rewards Multiplier. This adjustment factor is a function of the percentage deviation of the remaining epoch rewards from the target epoch rewards remaining. It evaluates to 1 if the remaining epoch rewards are at the target and to smaller (or larger) than 1 if the remaining rewards are below (or above, respectively) the target. This creates a drag towards the target schedule.
The sensitivity of the adjustment factor to the percentage deviation from the target are governable parameters: one for an underspend, one for an overspend.